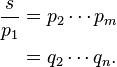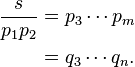|
|
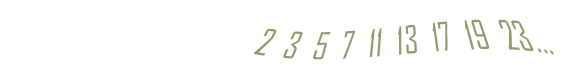
|
| Operations with prime numbers | ||||||||
| ||||||||
|
| ||||||||
| Prime numbers factorization | ||||||||
| ||||||||
|
Fundamental theorem of arithmetic The fundamental theorem of arithmetic states that every integer either is prime itself or is the product of prime numbers, and that this product is unique. Proof The proof uses Euclid's lemma: if a prime p divides the product of two natural numbers a and b, then either p divides a or p divides b (or both). Existence We need to show that every integer greater than 1 is a product of primes. By induction: assume it is true for all numbers between 1 and n. If n is prime, there is nothing more to prove (a prime is a trivial product of primes, a "product" with only one factor). Otherwise, there are integers a and b, where n = ab and 1 < a = b < n. By the induction hypothesis, a = p1p2...pj and b = q1q2...qk are products of primes. But then n = ab = p1p2...pjq1q2...qk is a product of primes. Uniqueness Assume that s > 1 is the product of prime numbers in two different ways: We must show m = n and that the qj are a rearrangement of the pi. By Euclid's lemma, p1 must divide one of the qj; relabeling the qj if necessary, say that p1 divides q1. But q1 is prime, so its only divisors are itself and 1. Therefore, p1 = q1, so that Reasoning the same way, p2 must equal one of the remaining qj. Relabeling again if necessary, say p2 = q2. Then This can be done for each of the m pi's, showing that m = n and every pi is a qj. Applying the same argument with the p's and q's reversed shows n = m (hence m = n) and every qj is a pi. "Fundamental theorem of arithmetic." Wikipedia, The Free Encyclopedia. 28 Sep. 2013. Web. 1 Nov. 2013. | ||||||||
|
| ||||||||
| Arithmetic operations with large numbers | ||||||||
| ||||||||
|
| ||||||||
| What is a prime number? | ||||||||
|
A prime number (or a prime) is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example, 5 is prime because 1 and 5 are its only positive integer factors, whereas 6 is composite because it has the divisors 2 and 3 in addition to 1 and 6. The fundamental theorem of arithmetic establishes the central role of primes in number theory: any integer greater than 1 can be expressed as a product of primes that is unique up to ordering. The uniqueness in this theorem requires excluding 1 as a prime because one can include arbitrarily many instances of 1 in any factorization, e.g., 3, 1 x 3, 1 x 1 x 3, etc. are all valid factorizations of 3. The property of being prime (or not) is called primality. A simple but slow method of verifying the primality of a given number n is known as trial division. It consists of testing whether n is a multiple of any integer between 2 and sqrt(n). Algorithms much more efficient than trial division have been devised to test the primality of large numbers. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. There are infinitely many primes, as demonstrated by Euclid around 300 BC. There is no known useful formula that sets apart all of the prime numbers from composites. However, the distribution of primes, that is to say, the statistical behaviour of primes in the large, can be modelled. The first result in that direction is the prime number theorem, proven at the end of the 19th century, which says that the probability that a given, randomly chosen number n is prime is inversely proportional to its number of digits, or to the logarithm of n. Many questions regarding prime numbers remain open, such as Goldbach's conjecture (that every even integer greater than 2 can be expressed as the sum of two primes), and the twin prime conjecture (that there are infinitely many pairs of primes whose difference is 2). Such questions spurred the development of various branches of number theory, focusing on analytic or algebraic aspects of numbers. Primes are used in several routines in information technology, such as public-key cryptography, which makes use of properties such as the difficulty of factoring large numbers into their prime factors. Prime numbers give rise to various generalizations in other mathematical domains, mainly algebra, such as prime elements and prime ideals. "Prime number." Wikipedia, The Free Encyclopedia. 22 Oct. 2013. Web. 1 Nov. 2013. | ||||||||
|
| ||||||||
| Home Integer factorization List of prime numbers Prime number theorem Formula for primes Euclid's theorem Sieve of Eratosthenes Largest known prime number Twin prime Mersenne prime Primality test Fibonacci prime Prime gap Wilson prime Ulam spiral Prime-counting function Privacy policy |